tougenkyou

competitive-programming

ABC276D

Find out how many times 2 and 3 respectively, are present in the prime factorization of the numbers in a.

Suppose a is all multiples of 7; e.g. 21, 14, 28

21 -> 3 * 7
14 -> 2 * 7
28 -> 2 * 2 * 7

If after removing all 2s and 3s from the prime factorization, we are left with the same common denominator, then we are able to arrive at the same number purely through dividing by 2 or 3.

no amount of dividing by 2 or 3 will turn 35 into 7.

import sys, math
n = int(input())
a = map(int, input().split())
 
g = set()
min_twos, min_threes = math.inf, math.inf
z = []
for num in a:
  cp = num
  twos = 0
  threes = 0
 
  while cp % 2 == 0:
    cp //= 2
    twos += 1
 
  while cp % 3 == 0:
    cp //= 3
    threes += 1
  
  # rmdr = num // (2**twos) // (3**threes)
  # g.add(rmdr)
  g.add(cp)
  if len(g) == 2:
    print(-1)
    sys.exit()
  
  min_twos = min(min_twos, twos)
  min_threes = min(min_threes, threes)
  z.append((twos, threes))
 
  # print("debug", num, twos, threes, rmdr)
 
res = 0
for tw, tr in z:
  res += (tw - min_twos) + (tr - min_threes)
 
print(res)

then keep track of the minimum number of twos and threes that make up any of the numbers in a.

Optimization

If you divide all the numbers by their collective GCD,

you necessarily remove as many twos and threes as possible from the prime factorization, along with other prime numbers.

Simply check if, after trying to remove any more 2s and 3s, the result is 1, which would indicate that

import sys, math
n = int(input())
a = list(map(int, input().split()))
 
_gcd = 0
for num in a:
  _gcd = math.gcd(num, _gcd)
 
# print("gcd is", _gcd)
res = 0
for num in a:
  cp = num // _gcd
  # twos = 0
  # threes = 0
 
  while cp % 2 == 0:
    cp //= 2
    res+=1
 
  while cp % 3 == 0:
    cp //= 3
    res+=1
  
  if cp != 1:
    print(-1) # that means the prime factorization includes numbers
    # other than 2 or 3
    sys.exit()
 
  # print("debug", num, twos, threes, rmdr)
 
print(res)

Takeaways

GCD of x and 0 is x. This can be used to find the GCD of all numbers in an array.

_gcd = 0
for num in a:
  _gcd = math.gcd(num, _gcd)

It is obvious that some prime factorization might be needed. No need to overcomplicate it, since trial division already runs in logarithmic time and has plenty of room to handle 1 <= a_i <= 10**9.

ABC274D

Key observation: consecutive line segments must be at a 90 degree angle -> whether you can reach X is independent of whether you can reach Y

each odd i in a_i is the absolute value of a vertical move, whereas each even i is the abs. val. of a horizontal move.

the upper bound of the range of possible positions is 1000 (N, the size of the moves array) * 10 (abs size of every move) * 2 (negative and positive).

multiply this by the size of the moves array again 1000 * 10 * 2 * 1000; 2 * 10**6 suggests dp[idx][position] is more than tractable, even if we do it twice for h and v.

Python 

import functools, sys
n, x, y = map(int, input().split())
a = list(map(int, input().split()))

# x, y is the target
h_moves = []
v_moves = []

for i in range(len(a)):
    if i & 1:
        v_moves.append(a[i])
    else:
        h_moves.append(a[i])

# print(h_moves, v_moves)

@functools.lru_cache(None)
def rech(idx, c):
    if idx == len(h_moves):
        return c == x
    return rech(idx + 1, c - h_moves[idx]) or rech(idx + 1, c + h_moves[idx])
    
x_ok = rech(1, 0 + h_moves[0])
# print(x_ok)

if not x_ok:
    print("No")
    sys.exit()

@functools.lru_cache(None)
def recv(idx, c):
    if idx == len(v_moves):
        return c == y
    return recv(idx + 1, c - v_moves[idx]) or recv(idx + 1, c + v_moves[idx])

y_ok = recv(0, 0)

print("Yes" if y_ok else "No")

CPP 

#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

int main() {
    int n,x,y;
    cin >> n >> x >> y;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    
    vector<int> h_moves;
    vector<int> v_moves;
    for (int i = 0; i < a.size(); i++) {
        // cout << "i " << i << endl;
        if (i & 1) {
            v_moves.push_back(a[i]);
        } else {
            h_moves.push_back(a[i]);
        }
    }
    
    int positivify = 1000 * 10; // the smallest possible coordinate is -10 * 1000 (-10 step size x 1000 times)
    vector<vector<bool> > dph(h_moves.size()+1, vector<bool>(1010 * 10 * 2, false)); // positive and negative...
    vector<vector<bool> > dpv(v_moves.size()+1, vector<bool>(1010 * 10 * 2, false)); // positive and negative...

    int abs_bound = *max_element(a.begin(), a.end()) * a.size();
    // int abs_bound = 10000;
    // the base cases
    dph[h_moves.size()][ x + positivify ] = true;
    
    for (int i = h_moves.size()-1; i >= 1; i--) {
        for (int j = -abs_bound; j <= abs_bound; j++) {
            // cout << "iterating over " << i << " " << j << endl;
            int jpos = j + positivify;
            if (jpos - h_moves[i] >= 0) dph.at(i).at( jpos ) = dph.at(i).at( jpos ) || dph.at(i + 1).at( jpos - h_moves[i] );
            if (jpos + h_moves[i] <= 1010 * 10 * 2) dph.at(i).at( jpos ) = dph.at(i).at( jpos ) || dph.at(i + 1).at( jpos + h_moves[i] );
        }
    }

    // for (auto& row : dph) {
    //     for (int i : row) {
    //         cout << i << ",";
    //     }
    //     cout << endl;
    // }

    if (!dph.at(1).at(h_moves[0] + positivify)) {
        cout << "No" << endl;
        return 0;
    }

    dpv[v_moves.size()][ y + positivify ] = true;
    for (int i = v_moves.size()-1; i >= 0; i--) {
        for (int j = -abs_bound; j <= abs_bound; j++) {
            // cout << "iterating over " << i << " " << j << endl;
            int jpos = j + positivify;
            if (jpos - v_moves[i] >= 0) dpv.at(i).at( jpos ) = dpv.at(i).at( jpos ) || dpv.at(i + 1).at( jpos - v_moves[i] );
            if (jpos + v_moves[i] <= 1010 * 10 * 2) dpv.at(i).at( jpos ) = dpv.at(i).at( jpos ) || dpv.at(i + 1).at( jpos + v_moves[i] );
        }
    }

    cout << (dpv[0][0 + positivify] ? "Yes" : "No") << endl;    
}

Takeaways

Fill the outer dimension first before the inner dimension (?)

Keep a "positivity" variable which will shift all the coordinates to start at 0, since we cannot access negative dp table indices.

Always check for out of bounds when populating the dp table by looping through every cell, even those at the edges.

ABC274D

Based on the constraints,

1 ≤ N ≤ 10**5  
0 < T ≤ 10**5  
0 ≤ X ≤ 4

one might think of arranging the snukes by time, and then choosing whether to visit or not to visit each Snuke or not.

However we would have to memoize both the current time, current index in the list of sorted snukes by time, AND X (which puts it at 5 * 10**10, thus intractable), because we need to know whether we can move to the current snuke or not.

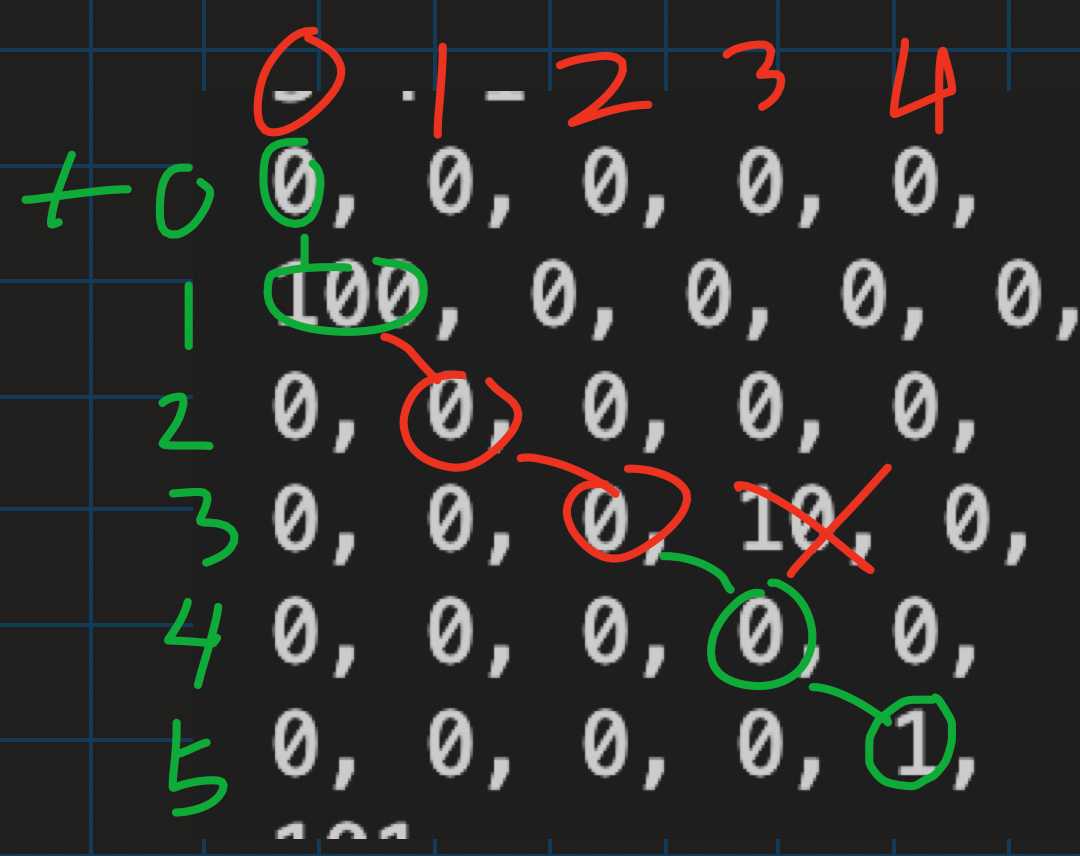
since our T goes only up to 10**5, we can iterate through every single time point from 0 to the max T. data representation for ABC274D

CPP 

#include <bits/stdc++.h>
typedef long long ll;

using namespace std;
int main() {
  int n;
  cin >> n;

  vector<vector<ll>> lookup(100002, vector<ll>(5, 0));

  int max_t = 0;
  for (int i = 0; i < n; i++) {
    int t, x, a;
    cin >> t >> x >> a;
    // cout << " gaga " << t << " " << x << " " << a << endl;
    lookup[t][x] = a;
    max_t = max(max_t, t);
  }

  // for (int i = 0; i <= max_t; i++) {
  //   for (int j = 0; j < 5; j++) {
  //     cout << lookup[i][j] << ", ";
  //   }
  //   cout << endl;
  // }
  
  vector<vector<ll>> memo(100002, vector<ll>(5, -1));

  function<ll(int, int)> rec = [&](int t, int x) -> ll {
    if (t > max_t) return 0;

    if (memo[t][x] > -1) return memo[t][x];
    ll acc = lookup[t][x];
    if ((x + 1) < 5)
      acc = max(acc, lookup[t][x] + rec(t + 1, x + 1 ) );
    if ((x-1) >= 0)
      acc = max(acc, lookup[t][x] + rec(t + 1, ( (x - 1 + 5) % 5) ) );
    acc = max(acc, lookup[t][x] + rec(t + 1, x));
    return memo[t][x] = acc;
  };

  cout << rec(0, 0) << endl;
}